Затухающие колебания

Корень из которых рассчитывается по следующей формуле

Содержание

Затухающие колебания – Колебания, энергия которых уменьшается со временем. Бесконечно долгий процесс вида невозможно в природе. Свободные колебания каждого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике мы обычно имеем дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Типичное демпфирование обусловлено силами сопротивления, которые обычно выражаются как линейная функция скорости колебаний или его площадь.

В акустике: демпфирование – это снижение уровня сигнала до полной неслышимости.

Дифференциальное уравнение затухающих колебаний в линейной системе:

Физические основы акустики зданий

Демпфирование – это постепенное ослабление колебаний с течением времени, вызванное потерей энергии в колебательной системе. При механической вибрации демпфирование вызывается силами трения и излучением колебательной энергии в окружающую среду в виде упругих волн. Свободные колебания всех реальных колебательных систем затухают.

Рассмотрим затухающие колебания линейной системы. Система называется линейной, если параметры, описывающие физические свойства системы, имеющие отношение к рассматриваемому процессу, не изменяются в ходе процесса.

Дифференциальное уравнение затухающих колебаний в линейной системе:

где ω – циклическая частота нестационарных собственных колебаний системы, δ (c -1 ) – коэффициент демпфирования.

Решение этого уравнения имеет вид:

Здесь – амплитуда затухающих колебаний, – циклическая частота затухающих колебаний.

В экспоненциальной форме уравнение затухающих колебаний записывается как:

Рис. 2 Диаграмма затухающих колебаний

Диаграммы затухающих колебаний

При наличии демпфирования собственные колебания (рис. 1) больше не являются гармоническими. Более того, затухающие колебания уже не являются периодическим процессом – трение влияет не только на амплитуду колебаний (т.е. является причиной затухания), но и на продолжительность затухания. По мере увеличения трения время, необходимое системе для совершения одного полного колебания, увеличивается. Диаграмма затухающих колебаний показана на рисунке 2.

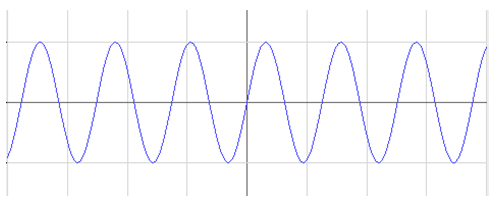
Рисунок 1: Диаграмма свободных гармонических колебаний

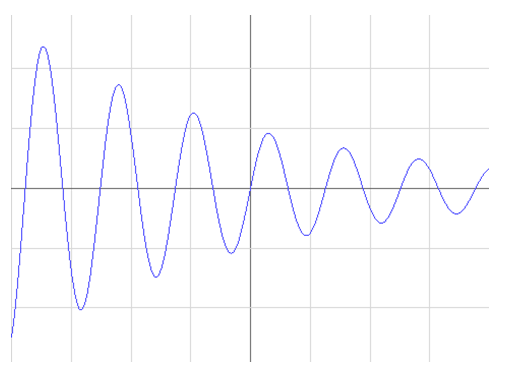
Рисунок 2: Диаграмма затухающих колебаний

Характерной особенностью колебательных систем является то, что небольшое количество трения влияет на период колебаний гораздо меньше, чем на амплитуду. Это сыграло важную роль в развитии часов. Первые маятниковые часы были построены голландским физиком и математиком Христианом Гюйгенсом в 1673 году. Этот год можно считать датой рождения современных часов. Ход маятниковых часов не очень чувствителен к изменениям из-за трения, которое в целом зависит от многих факторов, тогда как на скорость хода предыдущих часов без маятника трение влияло очень сильно.

На практике существует необходимость как в уменьшении, так и в увеличении демпфирования. Например, при разработке часовых механизмов целью является уменьшение затухания колебаний баланса. Для этого вал баланса оснащается острыми наконечниками, которые упираются в хорошо отполированные конические подшипники, изготовленные из твердого камня (агата или рубина). Напротив, во многих измерительных приборах очень желательно, чтобы подвижная часть устройства быстро позиционировалась во время измерения, но при этом совершая большое количество колебаний. Для увеличения демпфирования в этом случае используются различные демпферы – устройства, увеличивающие трение и потери энергии в целом.

называется амплитудой затухающего колебания, соответственно A₀– это начальная амплитуда. Амплитуда затухающего колебания уменьшается со временем и тем быстрее, чем больше коэффициент демпфирования.

Затухающие колебания.

1 Затухающие колебания заключаются в постепенном ослаблении колебаний с течением времени из-за потери энергии колебательной системой.

Свободные колебания реальных систем всегда затухают. Демпфирование свободных механических колебаний в основном обусловлено трением, сопротивлением окружающей среды и возбуждением упругих волн в среде. Демпфирование в системах электрических колебаний обусловлено тепловыми потерями в проводниках, образующих систему или находящихся в переменном электрическом поле, потерями энергии из-за излучения электромагнитных волн и тепловыми потерями в диэлектриках и ферромагнитах из-за электрического и магнитного гистерезиса.

Закон затухания колебаний зависит от свойств колеблющейся системы.

Система называется линейной, если параметры, связанные с физическими свойствами рассматриваемой системы, не изменяются в во время процесса.

Линейные системы описываются линейными дифференциальными уравнениями. Например, пружинный маятник, движущийся в вязкой среде, является линейной системой, если коэффициент сопротивления среды и упругость пружины не зависят от скорости и смещения маятника. Электрический колебательный контур можно считать линейной системой, если его электрическое сопротивление R, электрическая ёмкость С и индуктивность L не зависят ни от силы тока, ни от напряжения в цепи. В большинстве случаев реальные колебательные системы достаточно близки по своим свойствам к линейным системам.

Найдем дифференциальное уравнение, описывающее свободно затухающие колебания линейной системы. Для этого рассмотрим два примера линейных систем, механической и электрической, колебания которых сопровождаются диссипацией энергии.

Пример 1: Затухающие свободные колебания пружинного маятника массы m, движущегося в вязкой среде вдоль OX. На маятник действуют две силы: сила пружины F_{ведущий} и сила сопротивления среды F_cкоторую, как показывает эксперимент, можно считать в первом приближении пропорциональной скорости маятника v и направленной в на противоположную сторону от v: F_c= —bv, где b – постоянный положительный коэффициент пропорциональности, называемый коэффициентом сопротивления. Согласно второму закону Ньютона дифференциальное уравнение движения маятника имеет вид

Пример 2: Свободно затухающие колебания в электрическом колебательном контуре. Электрическое сопротивление реальной цепи равно R≠0, а согласно (27.22) колебания заряда конденсатора описываются уравнением

Уравнения (28.1) и (28.2) имеют одинаковый вид. Поэтому можно сделать вывод, что общее дифференциальное уравнение для свободно затухающих колебаний рассматриваемой системы линейные системы имеет вид

Здесь s – колебательно изменяющееся физическое свойство системы; ω – коэффициент демпфирования₀ – циклическая частота в свободном состоянии свободно демпфированный частота свободных незатухающих колебаний системы, т.е. при отсутствии потерь энергии (при ).

4 Затухающие колебания не являются периодическими, потому что максимальный значениеосциллирующей величины s, которая может быть достигнута в в некоторый момент времени t₁в более позднее время (в t>t₁) никогда не повторяется. С другой стороны, при затухающих колебаниях значение s стремится к нулю, изменяется в одном направлении (например, уменьшается) и достигает максимального и минимального значений w равный временные интервалы:

Значения Т и ω поэтому обычно называют периодом (условным периодом) и циклической частотой (условной циклической частотой) затухающего колебания.

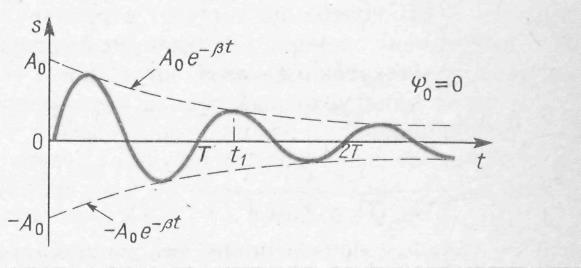
называется амплитудой затухающего колебания, соответственно A₀– это начальная амплитуда. Амплитуда затухающих колебаний уменьшается со временем, и тем быстрее, чем больше коэффициент затухания.

Интервал времени t, в течение которого амплитуда затухающего колебания уменьшается на коэффициент e, называется временем релаксации:

Логарифмический декремент затухания используется для количественной оценки скорости, с которой уменьшается амплитуда затухающего колебания.

Логарифмический декремент затухания – это безразмерная величина, равная натуральному логарифму отношения амплитуд затухающих колебаний в момент времени t i t+T (T-приблизительный период колебаний):

где N – это число колебаний, в течение которых амплитуда уменьшается в e раз. ,

Найдем зависимость между циклической частотой затухающих колебаний системы и логарифмическим уменьшением демпфирования .

Принудительная механическая вибрация

(1) Переменная внешняя сила, приложенная к системе и вызывающая ее вынужденные механические колебания, называется вынуждающей или возмущающей силой.

Дифференциальное уравнение вынужденных колебаний простейшей линейной системы, пружинного маятника, происходящих вдоль оси OX оси под воздействием переменной внешней силы F (t), Оно отличается от (28.1) только правой частью, которая равна соотношению F_x (t) к массе маятника m

Если F_x (t) – является периодической функцией времени, то при приложении этой силы к маятнику сначала возникает переходный режим вынужденных колебаний, при котором маятник участвует одновременно в двух колебаниях:

Первый член соответствует свободно затухающим колебаниям маятника (28.9) 1) :

Второй член соответствует незатухающим периодическим колебаниям маятника с частотой, равной частоте возмущающей силы F_x (t).

Значение амплитуды х₁ (t) равна A₀ β t , уменьшается более или менее быстро после начала вынужденных колебаний:в течение времени τ₀ =4.6/β амплитуда х₁ (t) уменьшается в 100 раз. В результате свободные колебания маятника практически завершаются через время t от начала колебаний: x (t) x₂ (t). Маятник переходит в устойчивое состояние вынужденных колебаний, совершаемых с частотой возмущающей силы.

Рассмотрим вынужденные колебания пружинного маятника под действием вынуждающей силы, которая изменяется по гармоническому закону с периодической частотой Ω:

где F₀ – амплитуда возбуждающей силы.

Покажем, что вынужденные колебания маятника в установившемся состоянии также являются гармоническими с той же частотой, т.е. найдем А и φ₀так, чтобы выражение

x = A cos (Ωt + φ₀) (28.21) преобразует уравнение (28.18) в тождество. Из (28.21) следует,

Заменим (28.21) и (28.22) в (28.18):

Здесь используются следующие сокращения:

Уравнение (28.23) показывает, что сумма трех одинаково направленных гармоник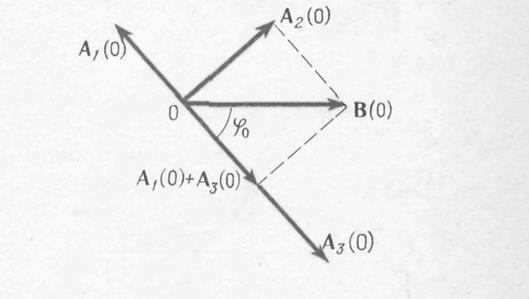

колебания с амплитудами А₁, А₂, Аз, с одинаковой циклической частотой Ω и разными начальными фазами (φ₀ +π, (φ₀ +π/2) должно совпадать с гармоническим колебанием происходящее вно по закону ВcosΩt. Мы будем использовать метод векторной диаграммы для суммирования этих трех колебаний. На рис. 28.3 показаны векторы амплитуд всех четырех колебаний в начальный момент времени A₁(0), А₂(0), Az(0)и B(0). Эти векторы должны удовлетворять условию (28.23), т.е.

С сайта Из рис. 28.3 и уравнений (28.24′) следует, что амплитуда А вынужденных колебаний в установившемся состоянии и фазовый сдвиг φ₀

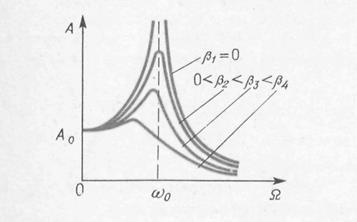
между смещением маятника из положения равновесия и вынуждающей силой зависит от отношения частоты циклических вынужденных колебаний Ω к частоте циклических незатухающих свободных колебаний ω₀а также коэффициент демпфирования β:

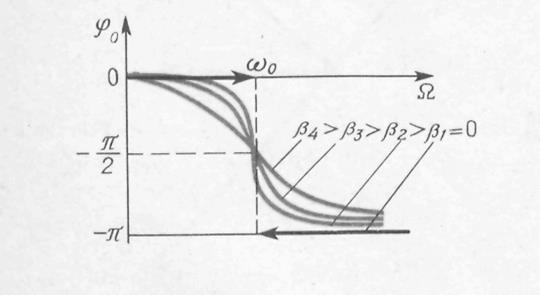
При Ω = 0 получаем φ₀(0)=0 и A(0)=A₀= F₀/(mω 2 )=F₀ /k – статическое смещение маятника из положения равновесия под действием постоянной силы F_x=Fo. В точке Ω амплитуда A (Ω) и tg φ₀ и φ₀ . Графики зависимости A (Ω) и φ₀ (Ω) при различных значениях коэффициента демпфирования β показаны на рисунках 28.4 и 28.5.

Добавление осцилляций

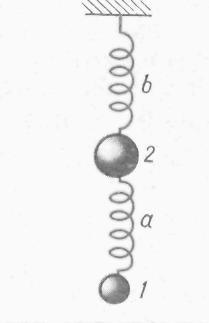
Под сложением колебаний понимается определение закона результирующих колебаний системы, когда эта система участвует одновременно в нескольких колебательных процессах. Различают два предельных случая: сложение колебаний с одинаковым направлением и сложение взаимно перпендикулярных колебаний. Первый случай соответствует, например, колебаниям вертикального груза 1 (рис. 27.7), который колеблется относительно вертикального веса 2 весной а и вместе с ним весной b. Этот же случай реализуется суперпозицией колебаний скалярных физических характеристик колеблющейся системы (давление, температура, плотность, ток и т.д.).

2 Сложение двух одинаково направленных гармонических колебаний

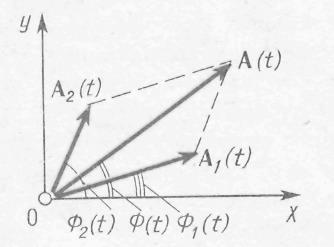
может быть выполнена с помощью векторных диаграмм. На рис. 27.8 показаны векторы A₁(t) и A₂ (t) амплитуд первого и второго колебаний в любой момент времени t, когда фазы этих колебаний равны F₁(t) = ω₁t + f₁ и F₂ (t) =ω₂t + φ₂. Результирующая вибрация s = s₁ +s₂ соответствует вектору A(t)= A₁ (t) + A₂(t), проекция которой на ось OK

s = A (t) sin F (t). (27.30)

Из теоремы косинусов,

Два колебательных процесса называются когерентными колебаниями, если они когерентны во времени так, что их разность фаз остается постоянной.

Разность фаз двух гармонических колебаний s₁ и s₂ равна .

Поэтому два гармонических колебания являются когерентными, если их циклические частоты одинаковы, т.е. разность фаз когерентных гармонических колебаний равна разности их начальных фаз: Ф₂ (t)-F₁ (t)=(ω₂-ω₁)t+(φ₂ – φ₁).

Соответственно, результирующие колебания являются гармоническими с одинаковой циклической частотой ω, т.е.

В зависимости от начальной разности фаз добавленных колебаний, амплитуда А результирующих колебаний изменяется в диапазоне

где m=0,1,2…- любое целое неотрицательное число. Если φ₂ – φ₁=±2mπ, то колебания находятся в фазе (являются вв фазе, и если φ₂ -φ₁= ± (2m+1)π

то они находятся в противофазе.

9. Сложение взаимно перпендикулярных колебаний циклических частот pω и qωгде p,q – целые числа:

Значения координат x u y точки колебаний М повторяются через равные промежутки времени T₀равна целому числу наименьшего кратного числа Т₁ = 2π/(pω) и T₂ = 2π(qω) – периоды колебаний вдоль оси OX и OY AXES. Следовательно, траектория точки М – представляет собой замкнутую кривую, форма которой зависит от соотношения амплитуд, частот и фаз начальных добавочных колебаний. Такие замкнутые траектории точки М, одновременно совершают гармонические колебания в двух взаимно

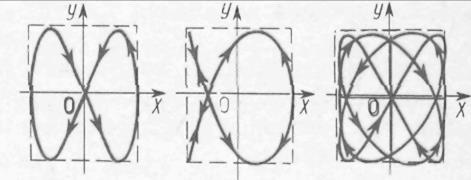перпендикулярные направления одновременно, называются фигурами Лиссажу. Фигуры Лиссажу вписаны в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны координатной оси OH и OY и расположены по обе их стороны на расстояниях, равных A₂ и А₁Отношение частот pω и qω добавочных колебаний равен отношению числа касаний соответствующей фигуры Лиссажу к стороне прямоугольника, параллельной оси OY, и сторона, параллельная OX. На рисунке 27.12 показан вид фигур Лиссажуса при трех различных значениях отношения q/p (2:1, 3:2, 4:3) и начальная разность фаз ∆ φ =φ₁ – φ₂=π/2.

1.Что изменится в уравнении гармонической вибрации, если вектор амплитуды на векторной диаграмме повернуть по часовой стрелке?

2.От чего зависят амплитуда и начальная фаза гармонического механического колебания?

3) Можно ли с помощью векторной диаграммы найти результат сложения трех одинаково направленных гармонических колебаний одинаковой частоты?

4) Как можно получить эллиптически поляризованные колебания?

5. как можно найти отношение частот дополнительных колебаний по форме фигуры Лиссажу? В каких случаях это можно сделать?

6. что подразумевается под спектром колебаний?

Упругая волна

называется Продольные, если частицы среды колеблются в направлении распространения волны.

Продольные волны связаны с объемной деформацией упругой среды и поэтому могут распространяться в любой среде – твердой, жидкой и газовой. Примером таких волн являются звуковые волны в воздухе.

Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространения волны.

Поперечные волны связаны со сдвиговой деформацией упругой среды и поэтому они могут создавать ираспространяются только в средах упругой формы, т.е. в твердых телах. Примером поперечных волн являются волны, распространяющиеся по струнам музыкальных инструментов.

Поверхностные волны – это особый случай поверхностные волны– Поверхностные возмущения, распространяющиеся вдоль свободной поверхности жидкости (или фазовой границы между двумя несмешивающимися жидкостями), вызванные внешнийОбразование и распространение этих волн определяется силами поверхностного натяжения. Силы поверхностного натяжения и гравитации играют решающую роль в формировании и распространении этих волн. В поверхностных волнах частицы жидкости совершают одновременные поперечные и продольные колебания, описывая эллиптические или более сложные траектории.

Среда называется однородной, если ее физические свойства, имеющие отношение к рассматриваемым проблемам, таковы не

§ 29.2.

Уравнение упругой волны представляет собой зависимость от времени и координат скалярных или векторных величин, характеризующих колебания среды при прохождении в ней рассматриваемой волны.

Например, для волн в сплошной среде такой величиной может быть вектор смещения частицы среды из положения равновесия или три его проекции на координатные оси. В случае продольных волн в газе или жидкости избыточное давление колеблющейся среды обычно равно разности между ее переменным давлением и равновесным давлением.

Распространение в упругой среде механических возмущений, индуцированных источником волн, связано с передачей волновой энергии. Поэтому такие волны, в отличие от стоячих волн (см. § 29.6), называются бегущими волнами.

Прямая линия, касательная которой в каждой точке совпадает с направлением распространения волны, т.е. с направлением передачи энергии волной, называется лучом.

В однородной среде лучи представляют собой прямые линии.

5. уравнение плоской синусоидальной волны,распространяющееся в непоглощающей среде вдоль положительного направления оси OX AXIS,

где A=const – амплитуда колебаний, называемая амплитудой волны;

ω = 2l/T – циклическая (круговая) частота волны;

Т– период колебаний; φ₀– начальная фаза колебаний в точках координатной плоскости х = 0. Значение F =ωt – ωt/v + φ₀равна фазе колебаний в любой точке на оси x х, называется фазой плоской волны.

Расстояние λ=vT, Длина волны, на которую распространяется синусоидальная волна за время, равное периоду колебаний, называется длиной волны.

Длина волны равна расстоянию между двумя ближайшими точками среды, в которых разность фаз колебаний равна 2π.

6.Помимо длины волны, еще одной характеристикой синусоидальной волны является волновое число,который показывает, сколько длин волн расположено на отрезке длиной 2 π:

Поэтому уравнение плоской синусоиды (29.4) можно также представить в виде

Соответственно, фаза этой плоской волны

Волновой вектор – это вектор по модулю k, равный волновому числу k и направлена вдоль луча в заданной точке М средний,

Волновой вектор плоской синусоидальной волны не зависит от выбора точки М. Для плоской волны, распространяющейся вдоль положительного направления OX, k – k и (i – орторомбический OX AXIS), поэтому kx = kg, где g – радиус-вектор точки М, и уравнение плоской волны (29.6) может быть записано в виде

s = A sin (ωt- кр + φ₀). (29.7)

Исходя из уравнения (27.5), волновое уравнение (29.7) можно записать в экспоненциальной форме, удобной для дифференцирования:

s = Ae i ( ω t- kr + δ) (29.7′)

Только вещественная часть комплексной величины š, т.е. количество s = Reš. Когда мы используем š для нахождения каких-либо волновых характеристик, необходимо отбросить мнимую часть комплексного выражения после всех математических операций.

Найдем выражение для скорости и продольный в однородной газообразной среде. Пусть газ находится в длинном горизонтальном цилиндрическом сосуде с подвижным поршнем площадью s. Первоначально поршень находится в покое, но в момент времени t он начинает двигаться и в течение небольшого промежутка времени dt он приобретает скорость dv₁и, таким образом, перемещается на расстояние dv₁dt/2. Пертурбативное действие поршня в момент времени dt распространяется в газе на расстояние v dt и охватывает область объемом Св. дт, где относительная объемная деформация

дополнительное давление dp, вызванное в газе движущимся поршнем, можно найти из закона Гука (29.1), где (DV/V) = dε:

Под действием силы dF = S dp газ, возмущенный поршнем, приобретает время dt импульс, равный dm dv₁/2, где dm =ρSv dt, ρ – плотность газа. Согласно второму закону движения Ньютона,

следовательно, желаемая скорость продольной волны в газе

Обратите внимание, что при выводе формулы (29.14) предполагалось, что плотность газа ρ -const. В газах это условие выполняется, если избыточное давление, связанное с распространением волны, во много раз меньше равновесного давления нетронутогоневозмущенного газа.

Формула (29.14) также справедлива для продольных волн в жидкости.

|Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения молекул, так и потенциальной энергией, возникающей в результате деформации. Если v₁-скорость колебаний частиц среды, массовая плотность кинетической энергии среды

где ρ – плотность среды; dW_K– кинетическая энергия всех частиц в малом объеме dV выбранной среды таким образом, что в ней скорость v₁ везде одинаково.

Можно доказать, что объемная потенциальная плотность энергии упруго деформированной среды

где dW_n– потенциальная энергия равномерно деформированного небольшого куска среды объемом dV; v-это фазовая скорость волны в среде; ε– относительная деформация.

Продемонстрируем справедливость уравнения (29.22) на примере продольной волны в газе. Элементарная работа, совершаемая внешними силами давления при деформации объема, δ A’= — p dV. Согласно закону Гука (29.1),

Эта работа заключается в увеличении потенциальной энергии упруго деформированной среды:

Соответственно, для конечной относительной деформации среды ε =ΔV/V

где, согласно закону Гука (29.1), ρ= -Kε. Следовательно, объемная плотность потенциальной энергии среды

Если учесть, что согласно (29.12), K=ρv 2 , то это выражение можно преобразовать к виду (29.22).

Под объемной плотностью энергии упругих волн понимается объемная плотность w механической энергии среды, обусловленной распространением этих волн, и равна сумме w_к и w_п:

Скорость передачи волновой энергии равна скорости движения в поверхностном пространстве, соответствующей максимальному значению объемной плотности w энергия волн. Для синусоидальных волн эта скорость равна фазовой скорости v.

Поток энергии dF_w через небольшой участок dS отношение энергии dW, передаваемых через эту зону в течение небольшого периода времени, к ее продолжительности дт:

Если v – вектор скорости передачи энергияволной, то dW равна энергии, заключенной внутри наклонного цилиндра, показанного на рис. 29.2, с площадью основания dS и длиной образующей vdt:

dW = wv dt dS cos α = w (v dS) дт,

где w – объемная плотность энергии волны; dS = n dS – вектор места dS; n – единичный вектор нормали к месту; а – угол между v и dS.

Вектор плотности потока энергии

U = wv. (29.29)

называется Умов вектор,как она была впервые представлена N. A. Умов (1874). Этот вектор направлен в сторону передачи энергии через волну и по модулю равен отношению потока энергии dF_w через малую площадь dS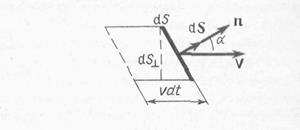

в область dS_┴ – проекция этой площади на плоскость, перпендикулярную направлению передачи энергии:

Поток энергии через любую поверхность S, мысленно проведенную в среде, подверженной волновому движению, равен потоку вектора Umov через эту поверхность:

3. простейшая группа волн – квазисинусоидальная плоская волна, возникающая в результате суперпозиции двух волн, распространяющихся вдоль оси АКСИС ОКС плоские волны с одинаковыми амплитудами и одинаковыми частотами и волновыми числами:

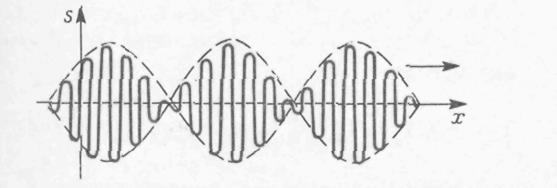
Зависимость s (x) в некоторый фиксированный момент времени t показана на рис. 29.4. Эта волна отличается от синусоидальной волны тем, что ее амплитуда

– является медленно изменяющейся функцией координаты х и время t.

Скорость этой несинусоидальной волны принимается равной и смещение точки М, при котором амплитуда А имеет определенное постоянное значение (например, A=0 или A = 2Ao). Таким образом, точка M движется по закону tdω – xdk = const, где

Это значение и называется групповой скоростью. Она равна скорости передачи

энергии, передаваемой квазисинусоидой. Групповая скорость u = d/dk подходит для описания передачи энергии (передачи сигнала) несинусоидальными волнами другого частотного спектра, при условии, что этот спектр не очень широк и дисперсия волн в среде для этих частот мала.

Найдем зависимость между группой и фазовой скоростью волны. Поскольку t

§ 29.6.

5. стоячие волны – это особый случай интерференции волн.

Стоячая волна – это волна, возникающая в результате суперпозиции двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковую частоту и амплитуду, а в случае поперечных волн – и одинаковую поляризацию (§ 29.2).

Поперечная стоячая волна создается, например, натянутой упругой струной, один конец которой неподвижен, а другой приведен в колебательное движение.

Суперпозицией двух когерентных бегущих плоских волн формы

где α – разность фаз волн в точках плоскости x = O, плоской синусоидальной стоячей волны, описываемой уравнением

Амплитуда стоячей волны A в отличие от амплитуды А бегущих волн является периодической функцией х:

Точки, в которых амплитуда стоячей волны A = 0 называются узлами стоячей волны, а точки, где амплитуда A_св. максимальна (A_ste =2А), называются лучами стоячей волны.

Положение узлов и скоплений определяется условиями

где m = 0, 1, 2. Расстояния между двумя соседними узлами и между двумя соседними пучками одинаковы и равны половине длины волны. Это значение называется длиной стоячей волны: λ_св. = λ/2. Расстояние между соседними узлами и лучом стоячей волны равно λ_{ст .} /2.

7. в стоячей волне (29.47) скорость колебательного движения частиц среды

v₁ =ds/dt = 2Aω cos (kx–a/2) cos (ωt +a/2), (29.50)

и относительная деформация среды

ε=ds/dx= -2Ak sin (kx+a/2) sin(ωt +a/2)=

2Ak sin (kx+a/2) cos(ωt +a/2+π/2) (29.51)

Поэтому, в отличие от движущейся волны, для которой справедливо соотношение (29.24), в случае стоячей волны ε предшествует v₁ по фазе на l/2, так что в моменты времени, в которые v_t достигает амплитудного значения, ε равно нулю и наоборот. Более того, амплитуды v₁ и ε зависят от координат х и, более того, по-разному:

пучки скоростей частиц и узлы деформации среды расположены в пучках стоячих волн, а пучки деформации и узлы скоростей расположены в узлах стоячих волн.

В упругой стоячей волне энергия периодически преобразуется из потенциальной энергии, расположенной в основном вблизи пучков деформации, в кинетическую энергию, расположенную в основном вблизи пучков скорости, и обратно. Поэтому энергия периодически мигрирует от узлов стоячей волны к ее пучкам и обратно. Однако плотность потока энергии одинаково равна нулю в узлах и в самих пучках. Периодическое среднее значение плотности потока энергии равно нулю в любой точке стоячей волны, потому что две волны, образующие стоячую волну, переносят равную энергию в противоположных направлениях в течение периода. Отсюда и название “стоячие волны”.

1 Возможна ли сходящаяся сферическая волна?

2. Что подразумевается под волновым уравнением и волновым уравнением?

3) От чего зависит фазовая скорость волн в в упругой среде зависит от?

&. Какими должны быть свойства среды, чтобы для механических волн в этой среде выполнялся принцип суперпозиции?

Какова связь между амплитудой синусоидальной волны в упругой среде и объемной плотностью энергии этой волны?

6. каков физический смысл групповой скорости?

7. В чем принципиальная разница между бегущей и стоячей волной? Каково значение вектора Умова в узлах и точках стоячей волны? Какова интенсивность стоячей волны?

Рассмотрим теперь преобразования различных форм энергии в процессе затухающих колебаний. Начальная энергия пружины Ò(

Слободянюк А.И. Физика 10/17.5

Рассмотренные свободные незатухающие колебания являются идеализацией, моделью, используемой для малых временных интервалов. В реальных механических колебательных системах обязательно присутствуют дисперсионные силы (силы трения, вязкие силы), приводящие к уменьшению механической энергии системы в результате ее преобразования в другие формы, например, в тепловую энергию. В этой главе мы рассмотрим описание колебательного движения в присутствии таких сил.

17.5.1 Демпфирование силами сухого трения.

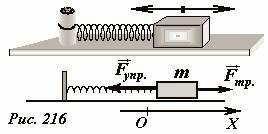
Рассмотрим характер движения пружинного маятника (рис. 216) при наличии силы сухого трения. Будем считать, что сила, действующая на брусок с горизонтальной поверхности, действует по закону Кулона-Амонтона. Обозначим через коэффициент трения μМы будем считать, что оно не зависит от скорости перемещения элемента, а также будем игнорировать разницу между трением скольжения и максимальным трением покоя.

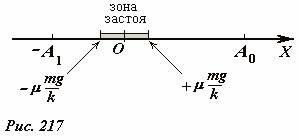
Выравнивание оси Ox с направлением движения бруса, а его начальная точка – с положением нерастянутой пружины. Если стержень отклоняется на расстояние xВ горизонтальном направлении на него действуют силы упругости и трения (рис. 217). Если в этом положении сила упругости (F_ = kx). меньше, чем максимальная сила трения покоя ≥ (F_ = ∗ mg), стержень будет находиться в состоянии покоя. Таким образом, в интервале, в котором k|x| < |mu mg|, или

Стержень может находиться в состоянии покоя, если его скорость равна нулю, поэтому этот интервал является зоной стагнации. Пусть начальный прогиб бруса составляет A₀ лежат вне зоны стагнации, предположим, что начальная скорость равна нулю. В этом случае уравнение движения стержня выглядит следующим образом (см. рис. 216)

ma = -kx + n mg. (2)

Обратите внимание, что это уравнение справедливо только для движения стержня влево, т.е. до тех пор, пока скорость стержня отрицательна υ < 0 – при изменении направления движения знак силы трения меняется [1] .

В этом заключается принципиальное отличие данного уравнения от уравнения движения массы, подвешенной на пружине (уравнение (7) из раздела 17.3.1), где постоянная сила мг действительно постоянна – не зависит от направления движения. Тем не менее, мы можем использовать рассмотренный ранее метод для решения уравнения (2), помня о его ограниченной применимости. Преобразуем уравнение (2) к виду

ma = -k ¯left (x – ¯frac ) . (3)

Это уравнение является уравнением гармонического колебания для величины (

x_1(t) = x – ﬁrac). Эта функция изменяется по гармоническому закону с частотой, равной частоте свободных колебаний пружинного маятника ¯.

¯omega = ¯sqrt< ¯frac>). С учетом начальных условий ¯(x(0) = A_0), ¯(¯) = 0), решение уравнения (3) имеет вид

x(t) – ﬁgure = ¯left (A_0 – ¯frac ¯ t = 0) ,

из которого следует закон движения стержня

x(t) = mu frac + Λ (A_0 – Λ ∗слева) ∗cos ∗omega t) . (4)

Скорость стержня будет изменяться по закону

∗upsilon(t) = -omega ¯left (A_0 – ¯frac ¯mega ¯left) ¯sin ¯omega t) . (5)

Полоса остановится в момент времени ¯(t_1 = ¯frac< ¯omega> < ¯omega>= ¯frac<2>) , где T – период собственных колебаний маятника. В точке остановки координата стержня будет равна

A_1 = x(t_1) = -A_0 + 2 frac) . (6)

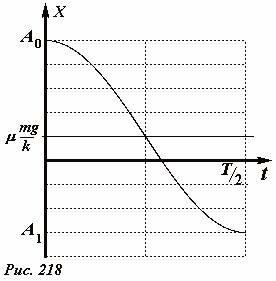
Обратите внимание, что координата точки остановки может быть положительной или отрицательной, в зависимости от величины начального отклонения. График закона на временном интервале (

t ™le ™frac<2>) построен на рисунке 218 и представляет собой отрезок косинуса, сдвинутый от начала координат на

™le ™frac). Если первая точка остановки не находится в зоне стагнации, бар начнет движение в противоположном направлении. Описание следующей фазы движения аналогично, и можно даже полностью использовать решение, полученное простым изменением направления оси.

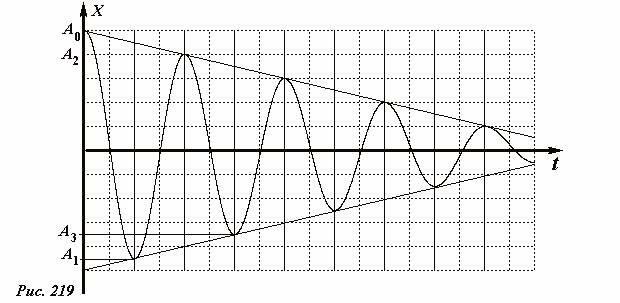
На рис. 219 показан график закона движения бруска при относительно небольшом коэффициенте трения, “сшитый” из сегментов синусоидальной волны, аналогичной рассмотренной выше. Между последовательными остановками прогиб стержня уменьшается на постоянную величину

∆Дельта |A| = 2 ∆frac) , (7)

пока следующая точка остановки не окажется в области стагнации.

Таким образом, сила трения постоянной модуляции не изменяет частоту колебаний, но уменьшает амплитуду колебаний, причем это уменьшение происходит по линейному закону.

В этом месте следует сделать филологическое замечание. Процесс затухающих колебаний не является периодическим, поэтому использование таких понятий, как период, частота, амплитуда колебаний, строго говоря, не оправдано. Однако для малого демпфирования эти понятия используются: в этом случае под переменной амплитудой колебания можно понимать отклонение от положения равновесия в точках остановки, период колебания можно рассматривать как интервал времени между двумя максимальными отклонениями (хотя и разными) в одном направлении. Конечно, при сильном трении (или небольшом начальном отклонении) движение может содержать только одну фазу: путь к остановке. Решите для себя, сколько должно быть оборотов – два или три, чтобы движение считалось колебательным.

Рассмотрим теперь преобразование различных форм энергии в процессе затухающего колебания. Начальная энергия пружины составляет (

U_0 = frac<ka^2><2>), полученная в результате работы внешней силы по отклонению стержня от положения равновесия, преобразуется в кинетическую энергию движения стержня в процессе движения и частично преобразуется в тепловую энергию из-за наличия трения.

Таким образом, при движении стержня от начального положения прогиба ¯ x = A_0) до края застойной зоны ¯(

x = A_0.n(x = A_0)) сила упругости больше силы трения. В этот момент происходят следующие энергетические процессы:

– Направление смещения совпадает с направлением силы упругости, поэтому сила упругости совершает положительную [2] работу ∆(∆дельта A_ = -kx delta x); – потенциальная энергия пружины уменьшается, изменение энергии пружины равно работе силы трения, взятой с противоположным знаком (вспомним очевидное: пружина совершает положительную работу, поэтому ее энергия уменьшается) (Дельта U = -дельта A_) = kx ∗ дельта x); – сила трения действует в направлении, противоположном направлению движения бруса, поэтому ее работа отрицательна ∗ (∗ дельта A_ = ∗ mg ∗ delta x); – количество выделившегося тепла равно работе силы трения, взятой с противоположным знаком, чем tr. Кинетическая энергия стержня увеличивается, и, согласно теореме о кинетической энергии, ее увеличение равно полной работе внешних сил, т.е. сумме сил упругости и трения.

■ дельта E_ = ∆дельта A_ + ∆дельта A_ = -kx delta x + m mg delta x ) . (8) – в любой момент времени сумма кинетической энергии стержня, потенциальной энергии пружины

а количество выделяемого тепла равно начальной энергии стержня (это следует непосредственно из уравнения (8)):

Процессы преобразования энергии в других элементах движения могут быть описаны аналогичным образом. Важно не забывать, что работа – это всегда мера передачи энергии из одной формы в другую.

Таким образом, используя закон сохранения энергии, легко получить координаты первой точки остановки. Учитывая, что в этот момент скорость и кинетическая энергия стержня равны нулю, запишем уравнение.

смысл которого можно выразить следующим образом [3]: сумма потенциальной энергии системы в момент остановки и количества выделившегося тепла равна начальной энергии системы. Из уравнения (10) следует уравнение (6) для первой координаты остановки.

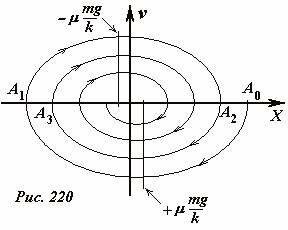
Уравнение закона сохранения энергии (9) позволяет построить фазовую траекторию движения стержня. Благодаря алгебраическим преобразованиям это уравнение преобразуется в

которое является уравнением эллипса, сдвинутого относительно начала координат. Уравнение справедливо для первой половины периода колебаний, дальнейшие участки строятся аналогично – результат показан на рисунке 220.

17.5.2 Демпфирование колебаний силами вязкого трения.

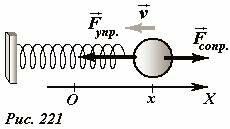
Силы вязкого трения являются еще одной распространенной причиной демпфирования вибрации. Для анализа этого типа движения рассмотрим колебательную систему, показанную на рис. 221. Предположим, что шарик движется по гладкой горизонтальной поверхности, но в процессе движения на него действует сила сопротивления окружающей среды (например, воздуха). Предположим, что эта сила пропорциональна скорости шарика

F = -beta vec . (1)

Векторная форма этого закона и отсутствие трения покоя позволяет рассматривать движение тела во всех его фазах, независимо от его направления. Коэффициент пропорциональности в формуле (1) зависит от свойств среды, размера и формы движущегося тела, в этой главе мы будем считать, что он, как и другие параметры системы, известен. Используя условные обозначения, запишем уравнение второго закона Ньютона в проекции на горизонтальную ось

ma = – kx – kx – ∆beta . (2)

Для общности слегка преобразуем это уравнение, разделив его на массу заряда

и ввести обозначения для появляющихся параметров. Значение (

∆frac = ™omega^2_0}) является квадратом круговой собственной частоты сферы (иногда называется собственная частота). Отношение коэффициента сопротивления к массе тела обозначается как [4] ∆(

frac beta> = 2 ∆frac) . В этом случае параметр γ называется коэффициент демпфирования. Можно отметить, что этот параметр имеет обратную временную размерность. Поэтому обратная величина времени равна ∆(beta^ <-1>= beta). Далее мы покажем, что это характерное время затухания колебаний. С этими обозначениями уравнение принимает вид

Это уравнение называется уравнение затухающих колебаний. Можно сказать, что изучаемое нами уравнение свободных колебаний (a = – omega^2_0 x) является частным случаем уравнения (3), в котором коэффициент затухания равен нулю. Поэтому при малом значении этого коэффициента решение уравнения (3) должно быть близко к гармоническому колебанию.

Как и раньше, неизвестным в уравнении (3) является функция x(t) – это зависимость координаты тела от времени. Кроме самой неизвестной функции, уравнение содержит ее первую (скорость) и вторую (ускорение) производные. Чтобы однозначно определить закон движения, необходимо добавить в это уравнение начальные условия. Предположим, что в момент времени t = 0 шарик отклоняется от положения равновесия на величину ∆(x(0) = A_0) и отпускается без толчка ∆(x(0) = 0).

Учитывая начальные условия, уравнение (3) может быть решено в явном виде, но процедура нахождения решения требует некоторой математической подготовки, поэтому мы опустим ее в нашем обсуждении. В явном виде решение уравнения (3) для заданных начальных условий и не слишком большой вязкой силы принимает вид [5].

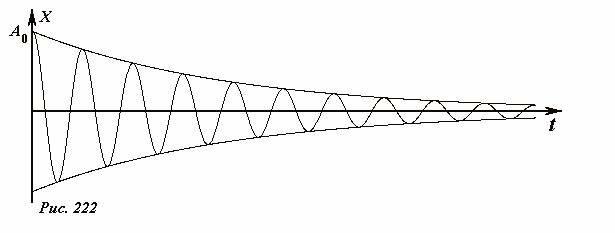
x(t) = A_0 e^ <- ∙gamma t> ∙cos ∙omega t) , (4)

Схема этой функции показана на рис. 222.

Отметим наиболее важные особенности решения уравнения затухающих колебаний (3). Наличие силы вязкого трения приводит к уменьшению амплитуды колебаний. В отличие от рассмотренного демпфирования, амплитуда нелинейно уменьшается под воздействием силы сухого трения. Далее мы покажем, что это распределение является геометрически прогрессивным. При наличии вязкого трения частота колебаний уменьшается по сравнению с частотой свободных колебаний. Качественно это снижение понятно: сила трения замедляет движение, что приводит к увеличению периода и уменьшению частоты. Если демпфирование невелико, этим изменением частоты можно пренебречь. Точная форма частотной зависимости коэффициента демпфирования дается уравнением (5). На рисунке 223 показано несколько графиков решения рассматриваемого уравнения при различных значениях коэффициента демпфирования. Цифры на графиках обозначают значение параметра (

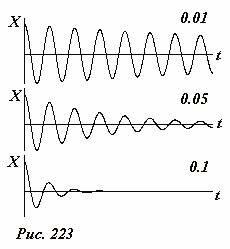
Следует отметить, что z γ ≥ ω₀ движение тела перестает быть колебательным. В этом случае (сильное затухание) тело монотонно движется к положению равновесия.

Давайте теперь проанализируем процесс затухания колебаний с энергетической точки зрения. Разделим область движения тела на небольшие интервалы Δx. В каждом интервале выполняется уравнение (3), которое мы умножаем на величину интервала Δx

имеет Δ x = -k x Δ x – ∆beta ∆upsilon Δ x) . (6)

Теперь объясним значение каждого термина в этом уравнении. Используя определения ускорения и скорости, преобразуем выражение в левой части

ma Delta x = m frac< Delta upsilon> < Delta t> Delta x = m Delta upsilon frac< Delta x> < Delta t>= m upsilon Delta upsilon = Delta left( frac <2> True> . (7)

Преобразование показывает, что эта величина является изменением кинетической энергии шарика. Первый член правой части представляет собой работу силы упругости в малом диапазоне смещения шарика и может быть представлен в виде

∆дельта A_ = F_ Delta x = -kx Delta x = ∆Delta ∆left( ∆frac <2> Вправо> . (8)

Результат очевиден: поскольку сила упругости потенциальна, работа этой силы равна уменьшению потенциальной энергии пружины.

Наконец, последний член – это работа силы вязкого трения. Эта сила не является потенциальной, поэтому ее работа не может быть выражена в терминах изменения потенциальной энергии. Работа силы трения, совершенная с противоположным знаком, равна количеству тепла, выделившегося за этот промежуток времени.

∆дельта Q = -дельта A_. = ∆бета ∆упсилон ∆дельта x . (9)

Поэтому уравнение (6) в форме

¯дельта Q = ¯дельта ¯левая( ¯frac <2>+ frac <2> Вправо> . (10)

допускает очевидную энергетическую интерпретацию: уменьшение механической энергии системы равно количеству выделяемого тепла.

При слабом демпфировании потери механической энергии можно аппроксимировать. Для этого мы воспользуемся общепринятым методом, который будем использовать и в дальнейшем. Еще раз преобразуем выражение для количества выделяемого тепла: используя соотношение ∆(∆delta x = ∆upsilon ∆delta t), перейдем от изменения координат к временному интервалу Δt

∆delta Q = ∆beta ∆upsilon ∆delta x = ∆beta ∆upsilon^2 ∆delta t) . (11)

Видно, что мощность выделяемого тепла пропорциональна квадрату скорости ∆(P = beta upsilon^2). Для того чтобы точно рассчитать потерю механической энергии (равную выделившемуся теплу), необходимо знать зависимость скорости тела от времени, т.е. закон движения, т.е. точно решить уравнение движения. Однако при малом затухании влиянием силы вязкого трения можно пренебречь на небольшом временном интервале [6] . Давайте продемонстрируем этот подход. Пусть po n вибрации амплитуда прогиба составляет A_n. Пренебрегая вязким трением, напишите закон движения для этого тела (изменение частоты также не учитывается):

x(t) ∆approx A_n ∆cos ∆omega_0 t ,

что соответствует следующей зависимости скорости тела от времени

¯upsilon(t) ¯approx -A_n ¯sin ¯omega_0 t) .

Следовательно, мощность излучаемого тепла изменяется во времени по закону

P = approx upsilon^2 = approx A^2_n omega^2_0 sin^2 omega_0 t) . (12)

Теперь легко найти среднюю мощность тепловых потерь за период колебаний

= ¯beta A^2_n ¯omega^2_0 < ¯sin^2 ¯omega_0 t> = ¯beta A^2_n ¯omega^2_0 < ¯frac<1 – ¯cos 2 ¯omega_0 t> <2>>> = ¯frac<1> <2>beta A^2_n ¯omega^2_0 ¯) . (13).

При выводе этого последнего соотношения учитывается, что среднее значение косинусов за период, очевидно, равно нулю.

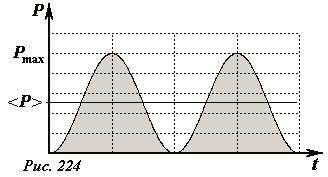
Учитывая, что в будущем нам придется многократно выполнять такое усреднение, ниже мы приводим еще одно явное геометрическое доказательство этого результата. Построим график мощности как функции времени ∆(P = P_ P = P^2 t). Площадь под графиком временной зависимости тепловой мощности (заштрихованная на рисунке) равна количеству выделившегося тепла. Проведение горизонтальной линии на половину максимальной мощности дает прямоугольник, площадь которого равна площади заштрихованной фигуры. Таким образом, значение (

Frac<1> <2>P_) равна средней мощности.

Таким образом, потеря механической энергии за один период колебаний составляет

∆Дельта E =

T = frac<1> <2>бета A^2_n frac^2_0 frac<2 frac<2 = ¯pi ¯beta A^2_n ¯omega^2_0 ¯) . (14).

Учитывая, что в моменты максимального отклонения скорость шарика равна нулю, из уравнения баланса энергии (10) получаем формулу, описывающую падение амплитуды на колебание

Frac <2>= E_n) – механическая энергия пружинного маятника после совершения n колебания. Изменение этой энергии описывается выражением из (15)

E_n – E_<n+1>= ¯pi ¯beta ¯omega_0 ¯frac<2 E_n>) . (16).

Коэффициент в правой части, с помощью введенных обозначений, преобразуем к виду

принимая во внимание то, что мы перепишем соотношение (16)

E_n – E_<n+1>= 2 ¯gamma T E_n> .

Из этого соотношения следует формула

E_<n+1>= (1 – 2 amma T) E_n) , что означает механическую энергию

указывая на то, что механическая энергия уменьшается экспоненциально

E_n = E_0(1 – 2 amma T)^n) . (17).

Используя связь между энергией и амплитудой, мы получаем однозначное выражение для изменения амплитуды

A_n = A_0 ¯left( ¯sqrt <1 – 2 ¯gamma T> ¯right ) ^n ¯approx A_0 (1 – ¯gamma T)^n) , (18)

который при построении использует приближенную формулу ((1 + ^xi)^ ^alpha ^approx 1 + ^alpha ^xi) для квадратного корня. Формула (18) показывает, что амплитуда колебаний также уменьшается в геометрической прогрессии. Безразмерная величина γT равно относительному уменьшению амплитуды за период колебаний.

Напомним, что полученные выводы справедливы для малых затуханий. Теперь мы можем дать количественный критерий малости демпфирования, описываемого уравнением (3): вышеприведенный вывод остается в силе, если выполняется условие

Механика состоит из трех частей: Кинематика, динамика и статика. Кинематика дает математическое описание движения, не касаясь его причин. Динамика – основная отрасль механики, изучает законы движения тел и причины, вызывающие движение и его изменения. Статика изучает законы равновесия системы тел под действием приложенных сил. Наше исследование будет ограничено двумя основными ветвями – кинематикой и динамикой.

Физика B1.B8.

Механика – это раздел физики, занимающийся изучением простейшего типа движения материи – механического движения – и причин, которые вызывают или изменяют это движение.

Механика состоит из трех частей: Кинематика, динамика и статика. Кинематика дает математическое описание движения без рассмотрения причин этого движения. Динамика – Основная отрасль механики, изучающая законы движения тел и причины, вызывающие движение и его изменения. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничим наше исследование двумя основными ветвями: кинематикой и динамикой.

Введение

Механика – это раздел физики, занимающийся изучением простейшего вида движения материи – механического движения – и причин, которые вызывают или изменяют это движение.

Механическое движение – это изменение во времени относительного положения тел или частей одного и того же тела. Причиной, которая заставляет тело двигаться или изменяться, является взаимодействие других тел.

Развитие механики началось еще в древние времена, но как наука она оформилась в Средние века. Основные законы механики были установлены итальянским физиком и астрономом Г. Галилеом (1564-1642) и английский ученый И. Ньютон (1643-1727).

Механику Галилея-Ньютона принято называть классическая механика. Изучает движение макроскопических тел, скорость которых намного меньше скорости света. с в вакууме. Законы движения тел со скоростями, близкими к скорости света, были сформулированы А. Эйнштейном (1879-1955) и отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и является основой релятивистской механики. Законы классической механики не подходят для описания движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех частей: Кинематика, динамика и статика. Кинематика дает математическое описание движения, не касаясь причин, порождающих это движение. Динамика – Основная отрасль механики, изучающая законы движения тел и причины, вызывающие движение и его изменения. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных ветвей – кинематики и динамики.

В механике для описания движения используются различные упрощающие модели, в зависимости от условий решаемой задачи: Материальная точка, идеально жесткое тело, идеально упругое тело, идеально неупругое телои т.д. Выбор той или иной модели продиктован необходимостью учесть в задаче все существенные особенности реальных движений и исключить несущественные, усложняющие решение.

Материальная точка – это тело, обладающее массой, размер и форма которого не имеют отношения к проблеме. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого каждое тело или тела в системе должны быть мысленно разбиты на большое число частей так, чтобы размеры каждой из них были пренебрежимо малы по сравнению с другими. по сравнению с размерами самих тел.

Абсолютно прочное тело – это тело, расстояние между любыми точками которого остается постоянным в результате движения или взаимодействия. Эта модель подходит, когда деформациями тела в движении можно пренебречь.

Абсолютно упругие и абсолютно неупругие тела – представляют собой два ограниченных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве задается положение тела, во времени происходит изменение положений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время – два фундаментальных понятия, без которых понятие движения теряет смысл: вне времени и пространства не может быть движения.

</n+1></n+1></n+1></ka^2>

Читайте далее: