Очевидно, что мгновенное значение тока через время T/2 от начальной точки графика будет равно нулю, а через время -T/4 его амплитудное значение. Ток также достигает своего пикового значения, но в обратном направлении, через время, равное 3/4 T.
Значение переменного тока (ЭДС, напряжения), соответствующее данному моменту времени, называется мгновенным значением
i, e и u – общие выражения для мгновенного тока, ЭДС и напряжения.
Мгновенное значение тока, как и значение амплитуды, можно легко определить с помощью графика. Для этого из любой точки на горизонтальной оси, соответствующей интересующему моменту времени, проведите вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной линии будет определять значение тока в этот момент, т.е. мгновенное значение тока.
Очевидно, что мгновенное значение тока будет равно нулю через время T/2 от начальной точки кривой, а через время T/4 – его амплитудное значение. Ток также достигает своего амплитудного значения, но в противоположном направлении, через время, равное 3/4 T.
Таким образом, график показывает, как ток в цепи изменяется во времени и что в любой момент времени существует только одно конкретное значение как величины, так и направления тока. Значение тока в данной точке цепи в данный момент времени будет точно таким же в каждой другой точке этой цепи.
Количество полных периодов, которые ток делает за 1 секунду, называется частота переменного тока и обозначается латинской буквой f.
Для определения частоты переменного тока, т.е, сколько периодов переменного тока происходит за 1 секундуразделить 1 секунду на время одного периода f = 1/T. Зная частоту переменного тока, мы можем определить его период: T = 1/f
Частота переменного тока измеряется с помощью единицы, называемой герц.
Если у нас есть переменный токЧастота переменного тока равна 1 герцу, а период переменного тока составляет 1 секунду. И наоборот, если мы имеем период переменного тока, равный 1 секунде, то частота такого тока будет равна 1 герцу.
Итак, мы установили параметры переменного тока — период, амплитуда и частота, — которые позволяют нам отличать друг от друга различные переменные токи, ЭДС и напряжения и при необходимости строить их графики.
При определении сопротивления различных цепей переменному току еще одной вспомогательной переменной, характеризующей переменный ток, является так называемая угловая частота или круговая частота.
Угловая частота обозначается ω и связана с частотой f соотношением ω = 2πf
Давайте объясним эту взаимосвязь. При построении графика переменной ЭДС мы увидели, что за один полный оборот рамы происходит полный цикл изменения ЭДС. Другими словами, чтобы совершить один оборот, т.е. повернуться на 360°, рамке требуется время, равное одному периоду, или T секунд. За 1 секунду кадр совершает поворот на 360°/T. Таким образом, 360°/T – это угол, на который поворачивается кадр за 1 секунду, и представляет собой скорость вращения кадра, которая называется угловая или вращательная скорость.
Однако, поскольку период T связан с частотой f соотношением f=1/T, круговая скорость также может быть выражена в терминах частоты и составляет ω =360°f.
Таким образом, мы приходим к выводу, что ω = 360°f. Однако для удобства использования круговой частоты во всех видах расчетов, угол 360°, соответствующий одному обороту, заменяется его радиальным выражением, равным 2π радиан, где π=3.14. Таким образом, окончательно получаем ω = 2πf. Следовательно, чтобы определить круговую частоту переменного тока (ЭДС или напряжения), мы должны умножить частоту в герцах на постоянное число 6,28.
– мгновенное значение тока ;
Альтернатор
Большая часть электроэнергии в современном мире вырабатывается генераторами переменного тока, которые производят гармонические колебания.
- генератор переменного тока
это электрическое устройство, преобразующее механическую энергию в энергию переменного тока.
Индуктивная ЭДС генератора переменного тока имеет синусоидальный закон
(e=
где ∆u200 ∆u200 E>_.
через рамку будет протекать переменный ток. Согласно закону Ома для данной цепи, ток в нагрузке составляет
{(i=dfrac
где ■(I_
Основными частями генератора являются (рис. 1):
- индуктор
– Электромагнит или постоянный магнит, создающий магнитное поле; - арматура
– Обмотка, в которой индуцируется переменная ЭДС; - щёточный коллектор
– Устройство, с помощью которого ток снимается с вращающихся частей или подается на них.
Рис. 1
Неподвижная часть генератора называется статор
а подвижная часть
ротор
. В зависимости от конструкции генератора переменного тока, якорь может быть либо ротором, либо статором. При генерации мощных переменных токов якорь обычно неподвижен, чтобы упростить схему передачи энергии в промышленную сеть.
В современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только один каркас (обмотку), мы получили бы переменный ток с частотой 1-2 Гц. Поэтому для получения переменного тока с промышленной частотой 50 Гц якорь должен содержать несколько обмоток, что позволяет увеличить частоту вырабатываемого тока. В паровых турбинах, где ротор вращается очень быстро, используется однообмоточный якорь. В этом случае скорость вращения ротора совпадает с частотой переменного тока, т.е. Ротор должен совершать 50 оборотов в секунду.
Генераторы большой мощности могут вырабатывать напряжение 15-20 кВ и имеют КПД 97-98%.
. Сначала Фарадей обнаружил лишь едва ощутимый ток в катушке, когда рядом с ней двигался магнит. “Какая от этого польза?” – спросили его. Фарадей ответил: “Какая польза может быть от новорожденного ребенка?”. Прошло чуть более полувека, и, по словам американского физика Р. Фейнмана, “бесполезный новорожденный ребенок превратился в чудесного гиганта и изменил лицо Земли так, как его гордый отец и представить себе не мог”.
*Принцип работы
Принцип работы генератора основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S
вращаются с угловой скоростью ω вокруг оси, перпендикулярной однородному магнитному полю индукции ∗ (∗vec).∗ (см. рис. 1).
Если рамка вращается равномерно, то угол α между направлениями вектора магнитной индукции ˆ (ˆvec и нормаль к плоскости рамы
= 0 и угол α0 = 0 (см. рис. 1), тогда
где ω – угловая скорость рамки, а ν – частота ее вращения.
В этом случае магнитный поток через рамку изменится следующим образом
ν =Bcos ¯ alpha =Bcos ¯omega ¯ t,¯)
Тогда, согласно закону Фарадея, возникает индуцированная ЭДС
∆(e= -Phi ‘(t)¯) = ˜sinus ¯omega ¯ t =
Обратите внимание, что ток в цепи течет в одном направлении в течение половины оборота рамки, а затем меняет направление, которое также остается неизменным в течение еще половины оборота.
Затем мгновенное значение напряжения:
То, что мы называем мгновенным значением напряжения eds
Переменный ток уже давно не имеет практического применения. Это было связано с тем, что первые электрогенераторы вырабатывали постоянный ток, чтобы соответствовать технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими управляющими свойствами. Однако по мере развития производства постоянный ток становился все менее полезным для удовлетворения растущих потребностей экономического энергоснабжения. Переменный ток сделал возможным эффективное распределение электроэнергии и изменение напряжения с помощью трансформаторов. Появилась возможность производить электроэнергию на крупных электростанциях, а затем экономично распределять ее среди потребителей, увеличивая тем самым радиус энергоснабжения.
Сегодня централизованное производство и распределение электроэнергии в основном основано на переменном токе. Цепи переменного тока (AC) имеют ряд особенностей по сравнению с цепями постоянного тока. Переменные токи и напряжения приводят к возникновению переменных электрических и магнитных полей. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают наиболее существенное влияние на процессы в цепях, усложняя их анализ.
Переменный ток (напряжение, ЭДС и т.д.) – это ток (напряжение, ЭДС и т.д.), который изменяется со временем. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодический, а наименьший интервал времени, в течение которого наблюдаются эти повторения, равен период T. Для периодического тока мы имеем
Обратной величиной периода является частота, измеряется в герцах (Гц):
Диапазон частот, используемых в технике: от сверхнизких частот (0,01 ¸ 10 Гц – в системах автоматического управления, в аналоговой компьютерной технике) – до сверхвысоких частот (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В Российской Федерации промышленная частота f = 50 Гц .
Мгновенное значение переменной является функцией времени. Обычно он обозначается строчной буквой:
i – мгновенное значение тока ;
u – мгновенное напряжение ;
е – мгновенное значение ЭДС ;
р – мгновенное значение мощности .
Наибольшее мгновенное значение переменной за период называется амплитудой (обычно обозначается прописной буквой и подстрочным индексом m ) .
среднеквадратичное значение переменного тока
Величина периодического тока, равная величине постоянного тока, который за один период производит тот же тепловой или электродинамический эффект, что и периодический ток, называется эффективная стоимость периодического тока:
Аналогично определяются эффективные значения ЭДС и напряжения.
Синусоидальный переменный ток
Из всех возможных форм периодических токов наиболее распространенным является синусоидальный ток. По сравнению с другими видами тока, синусоидальный ток имеет то преимущество, что он обычно позволяет наиболее экономично производить, передавать, распределять и использовать электроэнергию. Только при синусоидальном токе можно поддерживать постоянные формы напряжения и тока на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Представление синусоидальной ЭДС, напряжения
и токи в декартовой плоскости
Синусоидальные токи и напряжения могут быть представлены графически, записаны с помощью уравнений с тригонометрическими функциями, представлены как векторы на декартовой плоскости или как комплексные числа.
Графики двух синусоидальных форм ЭДС, показанных на рис. 1, 2 е1 и е2 соответствуют уравнениям:
Значения аргументов синусоидальных функций и называются фазы синусоиды, а значение фазы в момент ( t =0): и – начальный этап ( ).
Скорость изменения фазового угла называется угловая частота. Поскольку фазовый угол синусоиды в течение одного периода Т изменяется на рад, угловая частота равна , где f- частота.
Когда две синусоидальные величины одинаковой частоты рассматриваются вместе, разность их фазовых углов, равная разности их начальных фаз, равна фазовый угол.
Для синусоидальной ЭДС е1 и е2 фазовый угол:
Векторное представление синусоидально изменяющихся величин
различные количества
На декартовой плоскости из начала координат нарисуйте векторы, равные по модулю амплитудным значениям синусоидальных величин, и поверните эти векторы против часовой стрелки (в ПМТ это направление считается положительным) с угловой частотой, равной w . Фазовый угол при их вращении берется по положительной полуоси абсцисс. Проекции векторов вращения на оси ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Набор векторов, представляющих синусоидально изменяющиеся ЭДС, напряжения и токи, называется векторные диаграммы. При построении векторных диаграмм удобно размещать векторы для начального момента времени ( t =0), что следует из равенства угловых частот синусоидальных величин и эквивалентно тому, что декартова система координат вращается против часовой стрелки со скоростью w . Поэтому векторы неподвижны в этой системе координат (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их использование делает расчет схемы более четким и простым. Это упрощение заключается в замене сложения и вычитания мгновенных значений величин на сложение и вычитание соответствующих векторов.
Предположим, например, что в точке разветвления цепи (рис. 5) полный ток равен сумме токов двух ветвей:
Каждый из этих токов имеет синусоидальную форму волны и может быть представлен уравнением
Результирующий ток также будет синусоидальным:
Определение амплитуды и начальной фазы этого тока с помощью соответствующих тригонометрических преобразований оказывается довольно громоздким и не очень читаемым, особенно если складывается большое количество синусоидальных величин. Это гораздо проще сделать с помощью векторной диаграммы.
На рис. 6 показаны начальные положения векторов тока, проекции которых на оси ординат дают мгновенные значения токов для t =0. Поскольку эти векторы вращаются с одинаковой угловой скоростью w их относительные положения не меняются, а фазовый угол между ними остается равным.
Поскольку алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению полного тока, вектор полного тока равен геометрической сумме векторов тока:
Построение диаграммы масштабного вектора позволяет определить значение i из диаграммы, после чего решение о мгновенном значении можно записать, формально рассматривая угловую частоту: .
Представление синусоидальной ЭДС, напряжения
и токи с комплексными числами
Геометрические операции над векторами могут быть заменены алгебраическими операциями над комплексными числами, что в целом повышает точность получаемых результатов.
Каждый вектор в комплексной плоскости имеет комплексное число, которое можно записать как :
экспоненциальный
тригонометрические или
алгебраический – формы.
Например, ЭДС, показанная на рис. 7 вектором вращения, соответствует комплексному числу
Фазовый угол определяется проекциями векторов на оси “+1” и “+j” системы координат, как
Согласно тригонометрической форме обозначения, мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
Удобно представлять комплексное число как произведение двух комплексных чисел:
Параметр , соответствующий положению вектора для t =0 (или на вращающемся со скоростью w комплексной плоскости) называется комплексная амплитуда: а параметр это комплекс мгновенных значений.
Параметр оператор вращения вектор на угол w t относительно начального положения вектора.
В общем случае, умножение вектора на оператор вращения представляет собой его поворот относительно начального положения на угол ± a .
Поэтому мгновенное значение синусоидальной величины равно ее мнимой части без знака “j” произведение комплекса амплитуды и оператора вращения :
Переход от одной формы обозначения синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
Если, например, комплексная амплитуда напряжения задана как комплексное число в алгебраической форме:
– то для того, чтобы записать его в экспоненциальной форме, необходимо найти начальную фазу, то есть угол, образованный вектором относительно положительной оси полуоси +1:
Затем мгновенное значение напряжения:
При записи этого выражения предполагается, что , то есть, что представляющий вектор находится в первом или четвертом квадранте. Если , то во (втором квадранте)
и в (третьем квадранте)
Если мгновенное значение тока задано в виде , то комплексная амплитуда сначала записывается в экспоненциальной форме, а затем (при необходимости) с помощью формулы Эйлера переходим к алгебраической форме:
Следует отметить, что алгебраическая форма должна использоваться для сложения и вычитания комплексов, в то время как экспоненциальная форма удобна для умножения и деления.
Таким образом, использование комплексных чисел позволяет нам перейти от геометрических операций над векторами к алгебраическим операциям над комплексами. Таким образом, определяя комплексную амплитуду результирующего тока согласно рисунку 5, получаем:
Среднеквадратичное значение синусоидальной ЭДС, напряжений и токов
В соответствии с выражением (3) для среднеквадратичного значения синусоидального тока запишем:
Аналогичный результат может быть получен для синусоидальных ЭДС и напряжений. Поэтому среднеквадратичные значения синусоидальных токов, ЭДС и напряжений меньше их амплитудных значений в два раза:
Поскольку, как будет показано далее, энергетические расчеты цепей переменного тока обычно проводятся с использованием эффективных значений величин, по аналогии с предыдущим введем понятие комплекс эффективных значений
1. Основы Теория цепей : учебник для средних школ / Г.В. Зивеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. -Пятое издание, пересмотренное. -М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учебник для студентов вузов, изучающих электротехнику, энергетику и приборостроение. -Седьмое издание, переработанное и дополненное. М.: Высшая школа, 1978. -528с.
Проверьте вопросы и проблемы
1) Какова практическая цель представления синусоидальных величин векторами?
2. Каково практическое значение представления синусоидальных величин с помощью комплексных чисел?
3. каковы преимущества представления синусоидальных величин комплексами по сравнению с их векторным представлением?
(4) Для заданных синусоидальных функций ЭДС и тока напишите соответствующие комплексы амплитуд и среднеквадратичных значений, а также комплексы мгновенных значений.
где – коэффициент коэрцитивности катушки,- число витков катушки (рис. 5.2).
Постоянные и мгновенные значения тока, напряжения и силы тока
Поскольку ток, напряжение и ЭДС могут быть постоянными или переменными, для отражения этого факта используются различные символы.
Мгновенные значения тока, напряжения и ЭДС обозначаются строчными буквами, т.е. i, u, e.
Постоянные величины, т.е. те, которые не зависят от времени, обозначаются заглавными буквами I, U, E.
На рис. 4.3 показаны графики мгновенного значения тока и постоянного значения токаI.
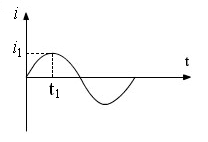

Рис. 4.3: Диаграммы переменного тока (a) и постоянного тока (b)
Сайт создан командой педагогов на некоммерческой основе для дополнительного образования молодежи.
Характерные величины синусоидальной ЭДС
Амплитуда – это максимальное значение периодически изменяющейся величины.
Амплитуды обозначаются заглавными буквами с кодом m, т.е. 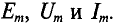
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений при повороте рамки на угол a = 90° или на угол a = 270°, поскольку 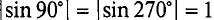 . Следовательно
. Следовательно 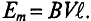
Затем 
Период – это время, в течение которого переменная совершает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Период обозначается буквой T и измеряется в секундах, с (сек), т.е. 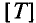 = с.
= с.
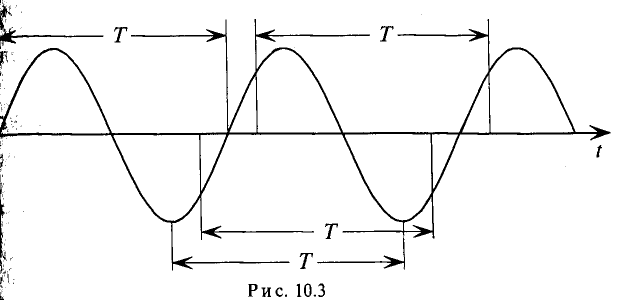
Значение ЭДС после каждого периода определяется по следующему уравнению (рис. 10.3):
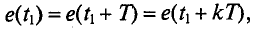
где k – целое число.
На рисунке 10.3 показана временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота – это количество периодов в единицу времени, т.е. обратная величина периода.
Обозначается буквой 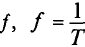 и измеряется в герцах (Гц):
и измеряется в герцах (Гц):
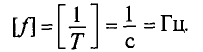
Стандартная частота в российских электросетях составляет 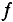 = 50 Гц. В системах электрического отопления используются следующие частоты
= 50 Гц. В системах электрического отопления используются следующие частоты 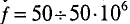 Гц (
Гц ( 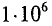 Гц = 1 МГц – мегагерц).
Гц = 1 МГц – мегагерц).
При частоте 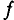 = 50 Гц, т.е. 50 периодов в секунду, период
= 50 Гц, т.е. 50 периодов в секунду, период
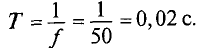
Угловая частота (угловая скорость) характеризует угол поворота кадра в единицу времени.
Угловая частота обозначается как 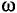 (омега):
(омега):

Угловая частота измеряется в единицах радианов в секунду, так же как угол измеряется в радианах (рад).
Поэтому за время одного периода T рамка повернется на 360° = радиан. Поэтому угловая частота может быть выражена следующим образом:

Мгновенное значение – это значение переменной в определенный момент времени.
Мгновенные значения обозначаются строчными буквами.
Из выражения (10.2) следует, что угол поворота рамки 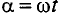 Мгновенные значения синусоидальных переменных могут быть записаны следующим образом:
Мгновенные значения синусоидальных переменных могут быть записаны следующим образом:
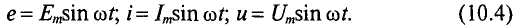
Таким образом, каждая синусоидальная величина характеризуется амплитудой и угловой частотой, которые постоянны для данной синусоиды. Следовательно, формулы (10.4) могут быть использованы для определения величины синусоиды в любой момент времени t, если известны амплитуда и угловая частота.
Фаза и фазовый сдвиг
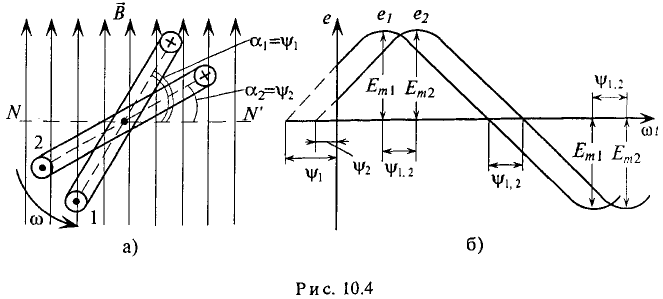
Если в магнитном поле две рамки, жестко соединенные друг с другом под определенным углом (рис. 10.4а), вращаются, то есть амплитуды ЭДС 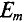 и их угловые частоты одинаковы, то мгновенное значение их ЭДС можно записать как
и их угловые частоты одинаковы, то мгновенное значение их ЭДС можно записать как
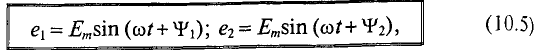
где 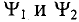 – углы, определяющие значения синусоидальных величин
– углы, определяющие значения синусоидальных величин 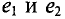 в начальный момент времени (t = 0), т.е.
в начальный момент времени (t = 0), т.е.
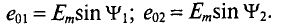
Таким образом, эти углы 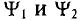 называются начальными фазами синусоиды.
называются начальными фазами синусоиды.
Начальные этапы 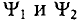 этих электромагнитных полей различны.
этих электромагнитных полей различны.
Поэтому, согласно (10.5) каждая синусоидальная величина характеризуется своей амплитудой 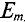 , угловая частота z и начальная фаза
, угловая частота z и начальная фаза 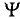 . Для каждой синусоиды эти величины
. Для каждой синусоиды эти величины 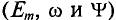 являются константами. В выражении (10.4) начальные фазы
являются константами. В выражении (10.4) начальные фазы 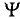 синусоиды равны нулю (
синусоиды равны нулю ( 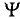 = 0).
= 0).
Значение 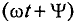 называется фазой синусоидальной волны.
называется фазой синусоидальной волны.
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет фазовый угол этих величин:

При вращении против часовой стрелки (рис. 10.4а) ЭДС в первом кадре достигает амплитуды и нулевого значения раньше, чем во втором кадре, т.е. 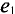 находится в фазе перед
находится в фазе перед 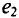 или
или 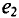 отстает по фазе
отстает по фазе 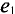 (Рисунок 10.46). Фазовый угол
(Рисунок 10.46). Фазовый угол 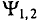 показывает угол, на который величина синусоиды опережает или отстает от другой, достигая своих амплитудных и нулевых значений раньше или позже).
показывает угол, на который величина синусоиды опережает или отстает от другой, достигая своих амплитудных и нулевых значений раньше или позже).
Две синусоидальные волны одинаковой частоты, которые одновременно достигают своих амплитуд и нулевых сечений, считаются согласованными по фазе (рис. 10.5a).
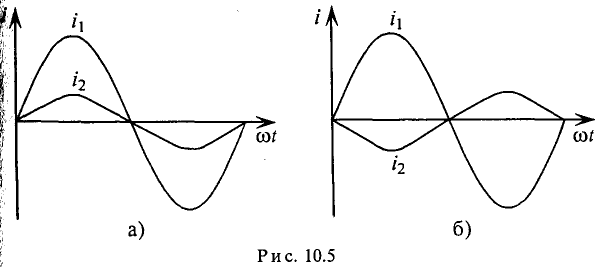
Если две синусоидальные волны одинаковой частоты одновременно достигают своих нулевого и амплитудного участков с разными знаками (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает другую и отстает от нее, является временем сдвига фаз 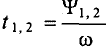 которая может быть выражена в терминах периода T и частоты
которая может быть выражена в терминах периода T и частоты 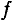 следующим образом:
следующим образом:
Средние и среднеквадратичные значения переменного тока
Помимо амплитудных и мгновенных значений, переменные токи, напряжения и ЭДС характеризуются также средними и эффективными (среднеквадратичными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно значению постоянного тока, при котором через поперечное сечение проводника протекает такое же количество электрической энергии Q, как и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току с точки зрения количества электрической энергии Q, протекающей через поперечное сечение проводника за определенный период времени.
Средние значения переменных токов обозначаются заглавными буквами через “s”, т.е. 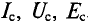 .
.
Если ток изменяется синусоидально, то в течение половины периода через поперечное сечение проводника в определенном направлении протекает определенное количество тока Q, а в течение другой половины периода через это же сечение в противоположном направлении протекает такое же количество тока. Поэтому среднее значение синусоидального тока за данный период равно нулю, т.е. 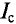 = 0.
= 0.
Таким образом, определяется среднее значение синусоидального тока в середине периода T/2, т.е.
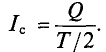
Из выражения (2.1) следует, что величина переменного тока 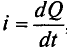 где
где 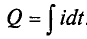 . Таким образом, среднее значение синусоидального тока
. Таким образом, среднее значение синусоидального тока 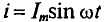 с начальной фазой
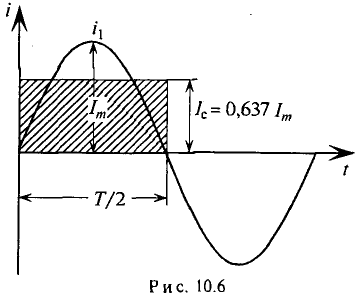
с начальной фазой 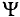 = 0 для половины цикла (рис. 10.6) определяется следующим образом
= 0 для половины цикла (рис. 10.6) определяется следующим образом
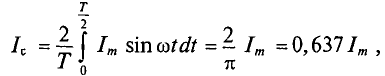
где 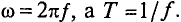
Графически среднее значение полупериода синусоидального тока равно высоте прямоугольника с основанием, равным T/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за полпериода (рис. 10.6).
Среднее значение переменной понимается как постоянная составляющая этой переменной.
Средние значения синусоидального напряжения и ЭДС за полупериод могут быть определены по аналогии с током.
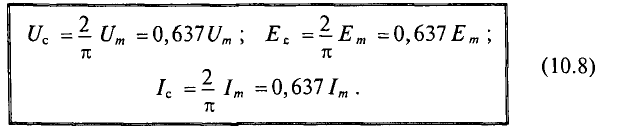
Эффективное значение переменного тока
Среднеквадратичное (или эффективное) значение переменного тока – это такое значение переменного тока, которое эквивалентно постоянному току с точки зрения тепла.
Среднеквадратичное значение переменного тока обозначается другими буквами без подписей: I, U, E.
Значение переменного тока I равно значению такого постоянного тока, который выделит такое же количество тепла в том же сопротивлении R, что и переменный ток, и за время, равное одному периоду первого тока T:
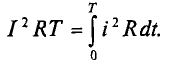
Следовательно, среднеквадратичное значение переменного тока
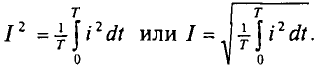
Если переменный ток изменяется синусоидально с начальным значением фазы, равным нулю, т.е. 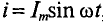 тогда среднеквадратичное значение такого синусоидального тока составит
тогда среднеквадратичное значение такого синусоидального тока составит
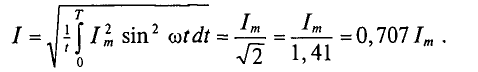
Среднеквадратичное значение синусоидального тока с 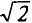 =1,41 от амплитудного значения. Также можно определить среднеквадратичные значения синусоидального напряжения и ЭДС.
=1,41 от амплитудного значения. Также можно определить среднеквадратичные значения синусоидального напряжения и ЭДС.
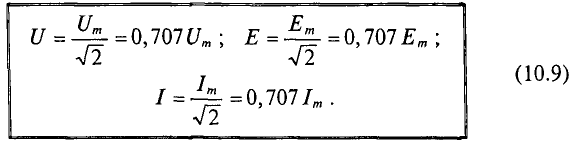
Номинальные значения тока и напряжения электрических цепей и оборудования выражаются их среднеквадратичными значениями.
Например, стандартные напряжения в электрических цепях, U = 127 В или U = 220 В, выражают среднеквадратичные значения этих напряжений. Изоляция должна быть рассчитана для амплитудных значений этих напряжений, т.е.
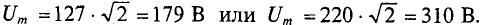
При расчетах и испытаниях цепей переменного тока чаще всего используются среднеквадратичные значения тока, напряжения и ЭДС.
Шкалы приборов для измерения переменного тока показывают среднеквадратичное значение переменного тока или напряжения.
Если не указано иное, среднеквадратичные значения тока, напряжения и ЭДС приведены в технической документации.
Коэффициенты формы и амплитуды
Отклонение кривых тока, напряжения и ЭДС от синусоидальной характеристики характеризуется коэффициентами формы 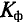 и амплитуда
и амплитуда 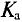 .
.
форм-фактор 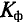 определяется как отношение эффективного значения переменной к ее среднему значению:
определяется как отношение эффективного значения переменной к ее среднему значению:

Форм-фактор необходимо учитывать при проектировании и испытании выпрямительного оборудования и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
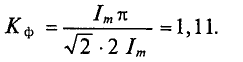
Коэффициент амплитуды 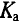 определяется отношением амплитудного значения переменной к ее среднеквадратичному значению:
определяется отношением амплитудного значения переменной к ее среднеквадратичному значению:

Для синусоидальных величин коэффициент амплитуды равен
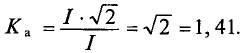
Чем больше фактор формы и фактор амплитуды, тем больше разница между 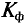 = 1,11 и
= 1,11 и 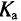 = 1,41, тем больше данная кривая отклоняется от синусоиды. Так, например, если
= 1,41, тем больше данная кривая отклоняется от синусоиды. Так, например, если 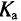 = 1,41, кривая имеет более острую форму, чем синус, а если
= 1,41, кривая имеет более острую форму, чем синус, а если 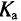
При копировании любых материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.
Сайт создан командой педагогов на некоммерческой основе для дополнительного образования молодежи.
Сайт написан, поддерживается и управляется командой учителей
Whatsapp и логотип Whatsapp являются торговыми марками корпорации WhatsApp LLC.
Данный веб-сайт носит информационный характер и ни при каких условиях не является публичной офертой в понимании статьи 437 Гражданского кодекса Российской Федерации. Анна Евкова не предоставляет никаких услуг.
Рисунок 3. Трехфазное сетевое напряжение
Однофазный переменный ток
ГЛАВА IV ОДНОФАЗНЫЙ ПЕРЕМЕННЫЙ ТОК
§ 48. ГЕНЕРАЦИЯ ПЕРЕМЕННОЙ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
Переменный ток – это электрический ток, величина и направление которого периодически меняются.
Переменный ток вырабатывается электромеханическими генераторами. Работа генератора основана на явлении электромагнитной индукции.
Рассмотрите принцип работы генератора переменного тока и используйте простейшую схему (рис. 46), чтобы объяснить, как генерируется переменная электроэнергия, под действием которой в цепи протекает переменный ток.
Магнитное поле генератора переменного тока индуцируется электромагнитом, по обмоткам которого протекает постоянный ток от внешнего источника электроэнергии. Катушка 3 из медного провода помещается в магнитное поле, закрепляется на оси 2 и вращается вокруг нее с помощью двигателя. Концы 4 и 7 катушки соединены с медными контактными кольцами 6, изолированными от оси. К кольцам прикреплены неподвижные щетки 5, к которым подключен электрический потребитель.
Известно, что величина индуктированной электродвижущей силы, возникающей в проводнике при прохождении через магнитный поток, зависит от магнитной индукции B, рабочей длины l
скорость и движение проводника в магнитном поле, а также синус угла между направлением движения проводника и направлением магнитного потока:
На рисунке 47 показаны различные положения катушки, вращающейся в однородном магнитном поле осциллятора с равномерной скоростью. В положении 1 катушка движется вдоль магнитного потока. Поэтому катушка не пересекает магнитных линий, угол ά между направлением движения проводника и магнитным потоком равен нулю, а sin 0° = 0. Следовательно, электродвижущая сила e = Blν
Виток, вращаясь по кругу, через некоторое время повернется на угол ά =90° и займет положение 2. При этом пересечется наибольшее число магнитных линий. Электродвижущая сила, индуцированная в катушке, будет наибольшей, sin 90°= 1 и e= Blν .
Из положения 2 катушка, продолжая вращаться, займет положение 3 и срежет магнитный поток под углом ά =180°. Индуцированная электродвижущая сила будет постепенно уменьшаться от положения 2 к положению 3 и будет равна нулю в положении 3, так как катушка не будет обрезать магнитный поток; sin 180°= 0 и e
=
Blν .
. sin 180°=0.
Используя правило правой руки, определите направление электродвижущей силы в катушке при ее перемещении в магнитном поле вдоль контура из положения в положение 3. Электродвижущая сила будет направлена от нас в сторону от плоскости рисунка. Предположим, что направление электродвижущей силы положительное.
Затем спираль будет последовательно вращаться до положения 4, 5 и вернется в положение 1
. Электродвижущая сила в катушке будет постепенно увеличиваться и станет наибольшей в положении 4 (ά = 270°), затем электродвижущая сила уменьшится и снова станет нулевой в положении 5
(sin 360° = 0). Затем весь процесс изменения э.ф. будет повторен.
Используя правило правой руки, можно увидеть, что при втором полуобороте катушки электродвижущая сила, генерируемая в катушке, изменит свое направление и будет направлена в нашу сторону. Предполагается, что направление электродвижущей силы отрицательное.
График изменения электродвижущей силы, возникающей в катушке, в зависимости от угла ее поворота в магнитном поле показан на рисунке 48.
Электродвижущая сила (рис. 48), которая изменяется по синусоиде, называется синусоидальной силой. синусоидальный
. Под действием этой электродвижущей силы в электрических цепях протекает синусоидально изменяющийся ток.
Предыдущая | Содержание | Следующая >>
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
- Шаговые двигатели: свойства и практические схемы управления. Часть 2.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Полное сопротивление цепи переменного тока – Основы электроники.
- Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
- Векторное и скалярное управление преобразователями частоты – принцип работы, система управления.
- Среднеквадратичное значение переменного тока следующее. Каково среднеквадратичное значение переменного тока?.